Above all shadows rides the Sun

and Stars for ever dwell:

I will not say the Day is done,

nor bid the Stars farewell

― J·R·R·托尔金，《魔戒：王者归来》

正如被晨曦拉长的幢幢高楼，正如夏日微风中的斑驳树影，是阴影让光变得更加跳脱、丰富。本文简述了在虚拟场景中模拟出真实世界的阴影效果的实时渲染方法——阴影映射（Shadow mapping）的基本原理和其相关算法，同时介绍了阴影映射算法存在的问题以及软阴影现象，希望能帮助大家对阴影映射有一个大概的认识。

月移疏影上东墙——简述阴影映射算法

如何模拟真实世界中的阴影？

在我们的宏观世界中，光沿着直线传播，并且会被物体吸收，同时形成反射和折射。对于阴影来说，我们只需要模拟光被物体吸收（挡住）就可以了。这要怎么做呢？

图1、阴影产生示意图

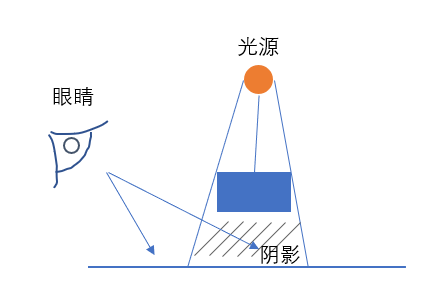
如图1所示，当眼睛看到的地方和光源之间有阻挡的时候，这个地方就处于阴影之中。我们在把一个场景画到屏幕的时候，就是把场景的一个个位置投射到屏幕的像素上；那么，对于画在屏幕上的每个像素对应的位置，都判断一下这个位置和光源之间有没有阻挡，不就可以知道这个位置是不是在阴影中了么？

是的，没错！你甚至可以只用二三十行shadertoy代码就实现这样的效果。但是这样做有一个问题，场景中的物体往往很复杂，判断有没有阻挡需要计算射线与场景中物体的相交，这是一个很费时的操作；一般来说，而如果在游戏中每个像素都这样做，那计算量就有些太大了，前一天的阴影还没画完，后一天太阳都出来了。有没有办法，不算射线与物体的相交，也能知道一个位置是否处于阴影之中呢？

阴影映射（Shadow Mapping ）的由来

什么是阴影映射？

在计算阴影时，我们是真的想知道光被什么东西挡住了么？不，我们只关心光是否被挡住。那么，其实我们只需要知道被计算的位置和光源之间有没有东西就可以了！

在将场景绘制到屏幕时，人们往往会记录一个像素对应的位置距离摄像机的距离（即深度），并把这些深度保存在一张和屏幕一样大的图片上以方便一些其他的计算，这样的记录深度的图被称作深度图（Depth map）。深度图的每个像素，记录了向这个像素的方向看过去的最近的距离。

图2、一个松鼠模型的深度图，颜色越白表示离相机越近 (图源：A Gauss-Newton Approach to Real-Time Monocular Multiple Object Tracking)

回到我们刚才计算阴影的问题，假如我们知道了对于光源来说各个方向的最近的距离，那么对于场景中的每个位置，我们都看它离光源的距离比这个最近距离大还是小，不就可以知道该位置是不是在阴影中了么——若离光源的距离大于对应方向的最近距离，则说明前面有东西遮挡；若离光源的距离等于对应方向的最近距离，说明该位置被光源照亮了，即没有阴影。

所以我们只需要在光源处，对场景计算一张深度图，对于场景中的每个位置，都把他投射到这张深度图上，将该位置的深度与深度图上对应像素的深度进行对比，就能知道这个位置是否处于阴影中。这种使用光源的深度图来计算阴影的方法，就叫做阴影映射，也就是Shadow mapping【1】，而这张深度图，则被称作阴影贴图（Shadow map）。

来看一个来自于维基百科的阴影映射的例子。图3(a)是一个有阴影的帕特农神庙模型，光源为在左侧向右照射的平行光。

(a)一个有阴影的“帕特农神庙” (b)无阴影 (c) 光源视角 (d) 阴影贴图图3、一个有阴影的“帕特农神庙”的计算过程

在使用阴影映射前，场景是没有阴影的，如图3(b)所示。要从图3(b)中得到图3(a)的结果，我们需要从光源处计算一张深度贴图。图3(c)即为从光源视角看向场景的样子。计算出来的阴影贴图为图3(d)，图3(d)和上面的图2的深度图一样，都是颜色越白，表示离观察点（图2为摄像机、图3(d)为光源）越近。有了深度贴图，那么就可以进行深度测试，判断图3(b)中的哪些像素是处于阴影中了，深度测试的结果见图4。有了图4，就能把渲染的结果，从图3(b)变为图3(a)了！

图4、在阴影贴图上深度测试失败的像素（图中白色部分），即处于阴影中的像素

总的来说，阴影映射是一个有两个渲染 pass 的算法：在第一个 pass，先在光源处，将场景物体离光源的深度写进阴影贴图；在第二个 pass，进行深度判断，将整个含阴影的场景渲染出来。

阴影映射的问题

不过现在，阴影映射还有一些很明显的问题没有解决：

一、走样（锯齿）问题

这是所有在屏幕空间使用离散缓存的算法都存在的问题：不论我们的阴影贴图有多大，它的分辨率总是有限的；而有限的分辨率，必定会在某些场合不够适用；对于阴影贴图来说，其表现就是出现阴影锯齿（Aliasing），或是走样的现象。

图5、有锯齿的阴影（图源：GPUGems - Chapter-11）

这种出现锯齿的表现误差，又被人们划分成了由透视产生的锯齿(Perspective aliasing)和由投影产生的锯齿(Projection aliasing)【2】。

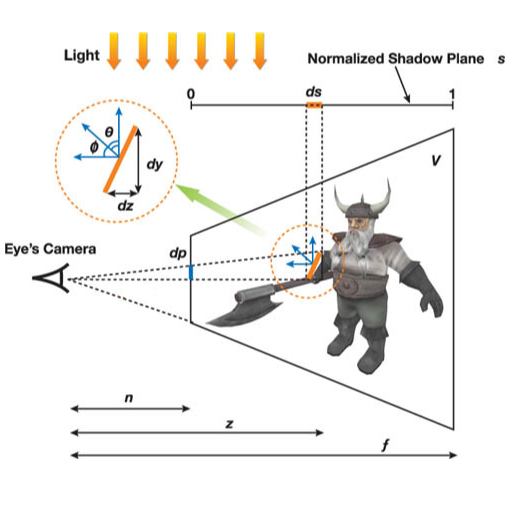
图6、阴影贴图锯齿的产生原因示意图（图源：GPUGems3 - Chapter 10）

图6解释了锯齿产生的原因：图6表示了一束平行光从上往下照射，相机位于左侧的场景，我们考虑图像中勇士的手臂的阴影；n表示相机的近平面的距离（假设屏幕绘制在近平面），f表示相机的远平面的距离，s为归一化后的阴影平面，z表示勇士手臂离相机的距离，ds是勇士手臂投影到在阴影平面上的长度，dp是勇士手臂投影到屏幕上的长度。此时，阴影贴图的走样误差（aliasing error）可以被表示为

$\frac{\mathrm{d}p}{\mathrm{d}s}=n\frac{\mathrm{d}z}{z\mathrm{d}s}\frac{\mathrm{cos}\phi}{\mathrm{cos}\theta}$

其中，

$\frac{\mathrm{d}z}{z\mathrm{d}s}$

是由透视产生的走样项，而

$\frac{\mathrm{cos}\phi}{\mathrm{cos}\theta}$

是由投影产生的走样项。

可见，由投影产生的锯齿是由光源位置、相机位置以及物体的几何（法线方向）决定的，而由透视产生的锯齿是由于透视的缩短现象造成的，所以人们研究 Shadow mapping 的锯齿问题（或分辨率问题），都是在尝试解决由透视产生的问题。比如：

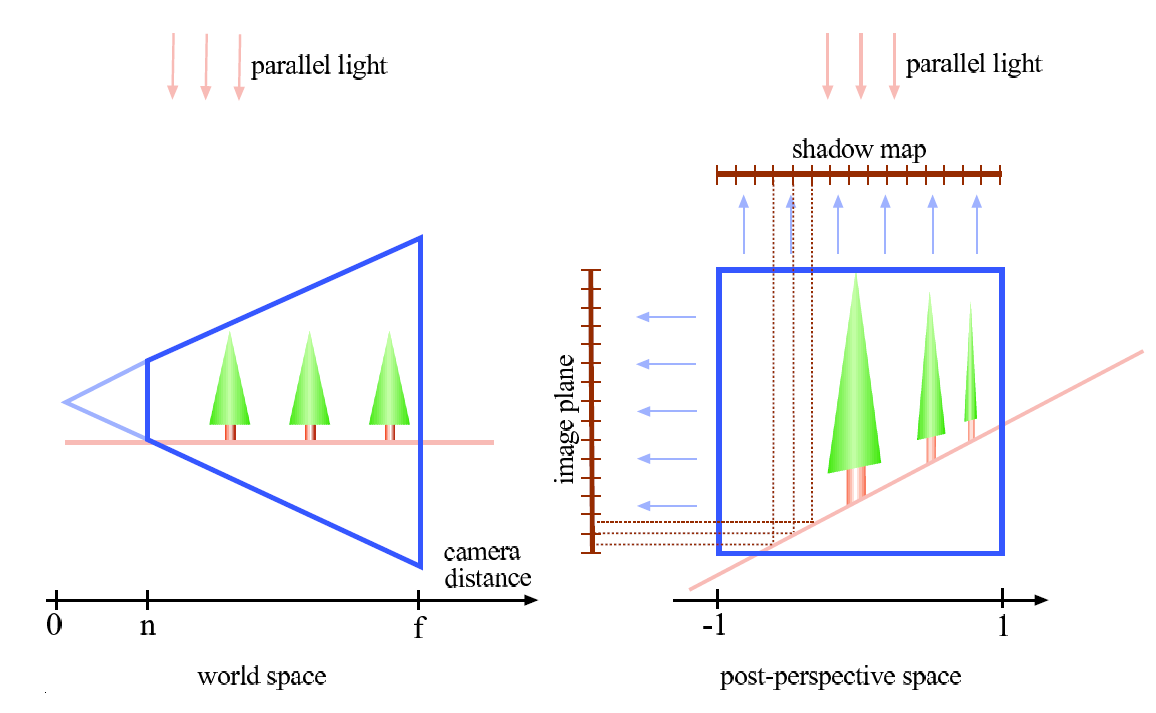
透视阴影贴图（perspective shadow maps ，PSM）【2】：在透视变换后的空间生成阴影贴图，大大减少了由透视产生的锯齿，并且更加充分的利用了贴图分辨率。

图7、左图为世界空间、右图为透视变换后的空间（图源：Perspective shadow maps）

使用多分辨率贴图的方法，如自适应阴影贴图（Adaptive Shadow Maps ，ASM）【3】。自适应阴影贴图通过量化阴影贴图的像素对最终绘制的图片的贡献，自适应地为需要高分辨率的地方计算高分辨率贴图，从而得到一个高质量的结果。这种方法更适用于离线渲染，而对于实时渲染来说效率有所不足。
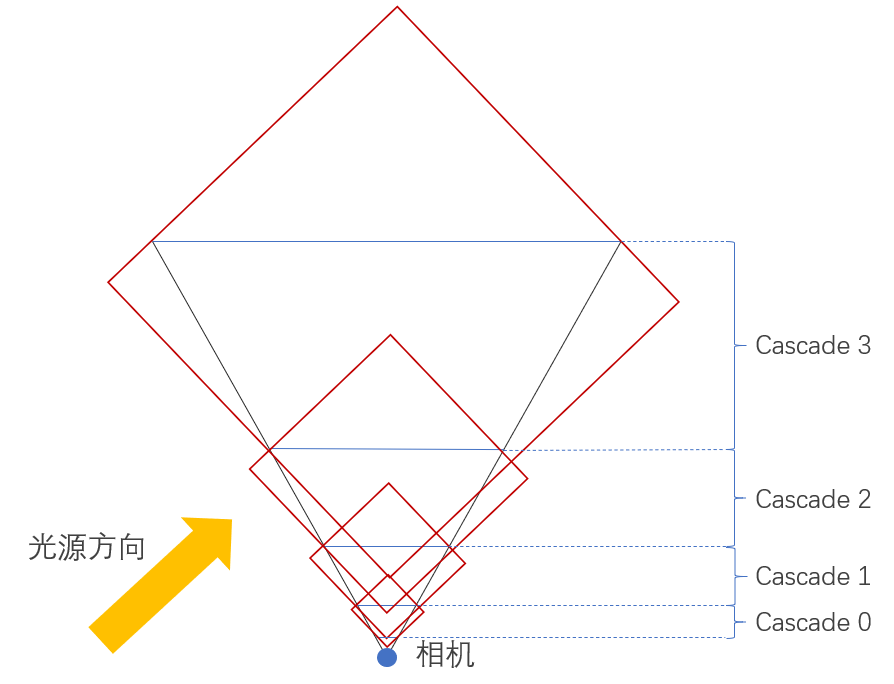
使用多张阴影贴图，来达到不同位置有不同分辨率的效果，这往往是大场景的动态阴影的解决方案。平行分割阴影贴图(Parallel-Split Shadow Maps，PSSM)【4】，又被称为级联阴影贴图(Cascaded Shadow Maps，CSM)是业界常用的方法。算法基于一个事实——物体离相机越远，绘制没有锯齿的物体阴影所需要的阴影贴图分辨率就越小。平行分割阴影贴图算法（PSSM）将相机视锥按不同的深度划分成几个部分，并以此去划分光源视锥；同时为了更大效率地利用贴图分辨率，PSSM还计算了场景的中物体的包围盒（Axis-aligned bounding box）来帮助光源视锥的划分（更一般的做法是直接求相机视锥划分后的包围盒）。光源视锥划分好后，再对每个划分的部分分别计算深度贴图，最后进行场景的渲染。由于不同的阴影层级之间使用了不同的阴影贴图，所以在不同层级的边界往往会出现阴影精度不连续的现象；从图8可以看出，不同的层级之间的阴影贴图是有重叠区域的，通过对层级边界的阴影在不同阴影贴图上插值，可以减弱阴影精度不连续的现象。

图8、级联阴影贴图示意图，图中相机视锥被划分为4个部分，红框为每个部分的光源视锥的包围盒

二、自遮挡及阴影脱离问题

除了锯齿现象，阴影映射算法（Shadow mapping）还有自遮挡（self occlusion）引发的阴影失真（Shadow acne）的问题。

图9：阴影失真问题（水壶：我挡我自己）（图源：http://ohyecloudy.com/pnotes/archives/377/）

如图9所示，虽然图片中的水壶的阴影被画了出来，但整个场景却被一道道奇怪的黑色条纹笼罩，仿佛有一层纱把灯挡住一样。这是为什么呢？

这也是因为我们的分辨率有限产生的。由于我们是用的阴影贴图来描述整个场景，每一个阴影贴图的像素对应了一块区域，而这块区域的深度被假设成一致的。图10描述了为什么这样会出现自遮挡的问题：图10中假设光源从左上照射向右下，照到了长条形的地板上；每个黄色的箭头，都对应一个阴影贴图的像素；图中蓝色的阶梯状边界，就是阴影贴图所表现的场景的深度。

图10、阴影失真原理示意图

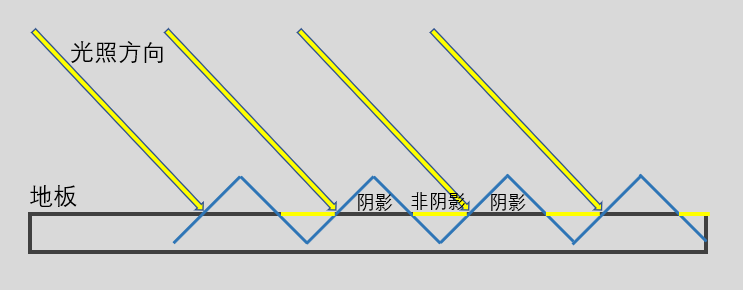
我们的地面是连续的，而阴影贴图的像素是离散的，贴图的深度只能看作是对连续的地面深度的近似。所以，可以看到在一个阴影贴图像素所表示的地面上，会同时存在阴影中和非阴影中两个状态；整个地面上，阴影区域和非阴影区域交替出现，形成自遮挡的现象。要怎么避免自遮挡现象呢？

当然了，如果光源方向完全垂直于地面的话，这个阶梯就和地面重合了，这种自遮挡现象自然就没有了；而对于不是垂直的情况，可以通过增加一个偏移来避免自遮挡——就是把这个蓝色的阶梯向光照方向移动一段距离，阴影的部分自然就少了，从而避免了自遮挡现象（图11）。

图11、增加偏移量以避免自遮挡现象

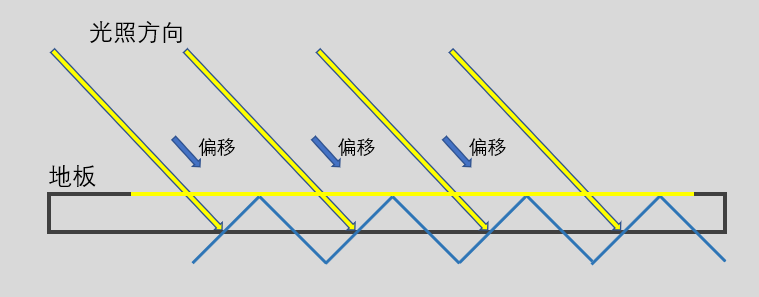
但是，把阶梯移动后，又有了新的问题：强行加上偏移，必然会使一些原本正确的阴影变的看不见了，这就是阴影脱离（Detached shadow）现象，人们又调皮的给了它一个另外的名字——彼得潘现象（Peter Panning）。

(a)增加阴影偏移后，脚的阴影消失（图源：Real-Time Rendering） (b)小飞侠彼得潘正尝试抓住自己的影子（图源：Walt Disney Productions）图12、阴影脱离（Detached shadow）现象

现在并没有一个好的解决阴影脱离现象的方法，只能尽量减少阴影偏移量，来避免阴影脱离现象过于明显。

从渲染方程的角度看 Shadow mapping

从我们上面的讨论可以发现，Shadow mapping 是将阴影的计算从渲染中分离了出来，算法先是计算了一个像素是否在阴影中（即对于光源的可见性），然后再将阴影的结果给到渲染的过程，从而得到最终的图像。那么，这样做是合理的么？是否存在一些情况，不能这样做呢？

在回答这些问题前，我们先来看一个积分的近似。

一个数学近似

对于连续的函数 f 和 g，在积分区间 $\Omega$ 上，由定积分的均值定理，存在 $a \in \Omega$ 满足下面这个等式：

$\int_{\Omega} f(x)g(x)\,\mathrm{d}x = f(a)\int_{\Omega}g(x) \,\mathrm{d}x$

如果我们用 $\frac{\int_{\Omega}f(x)\mathrm{d}x}{\int_{\Omega}\mathrm{d}x}$ 来近似 f(a) 的话，就得到了下面这个约等式：

$\int_{\Omega} f(x)g(x)\,\mathrm{d}x\approx\frac{\int_{\Omega}f(x)\mathrm{d}x}{\int_{\Omega}\mathrm{d}x}\cdot\int_{\Omega}g(x) \,\mathrm{d}x$

这个约等式在满足下面的任一条件的情况下会比较准确：

f(x) 的支撑集（Support）比较小，可理解为 f(x) 的积分域比较小。
g(x) 在积分区间内比较光滑（Smooth），即其值变化不大。

近似的渲染方程

渲染方程可以被写为：

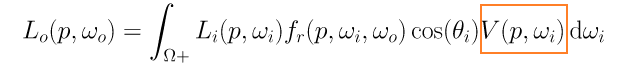
其中，橙色框里面为方程中的可见项（Visibility）。将上面的约等式套用至渲染方程，可以得到：

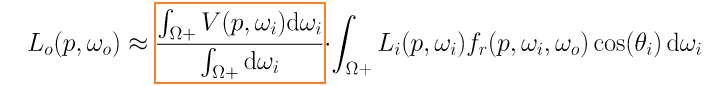
这个约等式把可见项从积分中单独拿了出来，可以先计算可见项，再计算光照相关的部分——这不就是我们的 Shadow mapping 的思路么？可见，这个近似正是 Shadow mapping 背后的原理。于是，可以知道 Shadow mapping 更适用于以下的情况：

$V(p, \omega_i)$ 的支撑集比较小的时候——即积分的范围比较小的时候。那么积分范围最小是什么时候呢？是积分范围为一个狄拉克δ函数的时候。这时，对应的是点光源，或方向光源（Directional Light）。
$L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) \cos(\theta_i)$ 比较光滑的时候。这一项和 $\omega_i$ 相关的有光源 $L_i(p, \omega_i)$ 和材质的BRDF项 $f_r(p, \omega_i, \omega_o)$ 。光滑的光照对应着光源范围内趋于固定的辐射值（Constant radiance area lighting），如一般的面光源；而光滑的BRDF对应着物体的材质趋于散射（Diffuse）材质。

软阴影算法

什么是软阴影？

观察上面的一些带阴影的例子，大家会发现这些阴影的边界非常清晰，阴影区域和非阴影区域有着很明显的分界线。这似乎和我们平时在生活中看到的阴影不太一样，为什么生活中的阴影往往有着模糊的边界呢？

这是因为，上面的例子中，我们使用的光源都是方向光源，它只能产生边界清晰的阴影。

图12、本影和半影

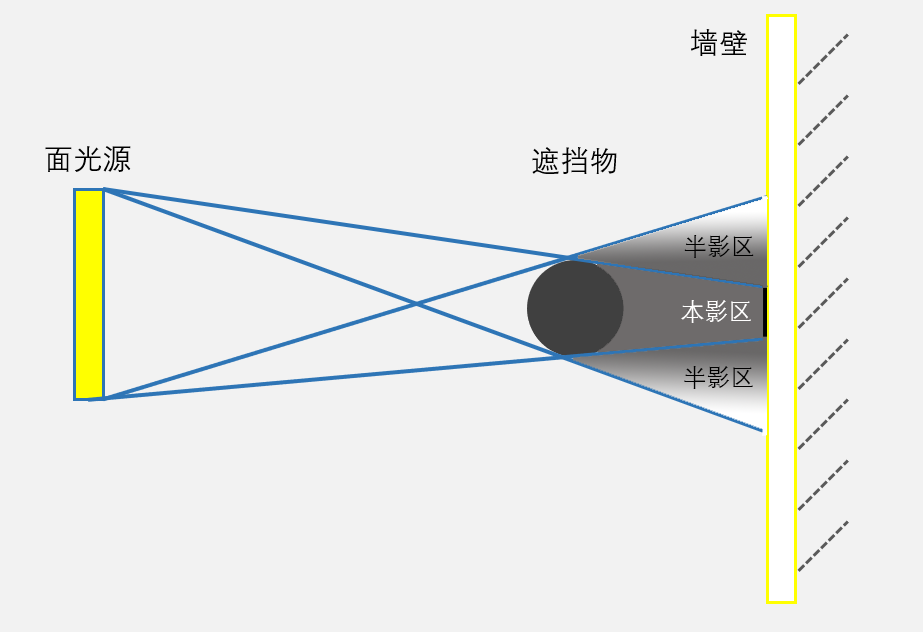
图12解释了对于更一般的面光源，阴影边界是过渡的，而不是突变的原因：在图12中，左侧光源是一个面光源，光被遮挡物（一个球）遮挡，而将阴影投射到墙壁上；可以发现，存在一些阴影区域，是完全不能接受到光的，这个区域被称作本影区（Umbra）；同时，也存在一些区域，只能接受到部分光源，这些区域被称作半影区（Penumbra）。在半影区，离本影区越近，接受到的光照就越少——这就是阴影逐渐从暗变为亮的原因。这种由于半影区域的存在而造成的存在过渡的阴影，被称为软阴影（Soft Shadows）。

阴影抗锯齿算法——Percentage Closer Filtering

为了在虚拟场景中也能绘制出软阴影，我们需要一些工具。Percentage closer filtering 是人们为了一定程度上解决阴影锯齿的问题而提出的算法——原本我们判断一个位置是否在阴影中，是将这个位置投影到阴影贴图上，根据阴影贴图上像素的深度来进行判断。这个过程一共只做了一次判断，判断的结果是非零即一的。为了让锯齿没那么明显，人们不仅仅使用这个位置对应的一个阴影贴图像素，而是看这个像素周围的一圈像素（比如说原像素周围的7x7范围），对这一圈像素都进行深度比较，将所有比较的结果进行平均，再作为这个位置的阴影比较结果。这样一来，像素的阴影计算就不再是非零即一的，而变成了在零到一这个区间中的一个值（比如用2x2的像素范围，就能得到 [0, 0.25, 0.50, 0.75, 1.0] 这5种值，分别对应[0个、1个、2个、3个、4个]像素不在阴影中），使得原来的锯齿边缘变得模糊；使用的范围（Filter size）越大，边缘就越模糊，模糊的范围也越大。

(a)平行光计算出来的人物阴影，在地面上存在明显的锯齿 (b) 使用了PCF后得到的人物阴影图13、PCF的抗锯齿效果(图源：Games202 Assignment 1)

假设我们渲染的像素是 x，x 对应到阴影贴图的位置是 p，x 对应的可见性为 V(x)，则PCF算法的核心思想可以用下面这个公式表示：

$V(x) = \sum_{q\in N(p)}w(p,q) \cdot \chi^{+}[D_{SM}(q)-D_{scene}(x)]$

其中，w(p, q) 是加权函数，N(p) 表示点 p 的邻域（即模糊使用的范围）； $D_{SM}(q)$ 表示 q 点对应的阴影贴图上的深度， $D_{scene}(x)$ 表示 x 对应位置到光源的深度，而 $\chi^{+}$ 是下面的这样一个简单函数：

$\chi^{+}(x)=\begin{cases}1, x>0\ 0, x\end{cases}$

题外话：或许有人会奇怪 Percentage Closer Filtering 这个命名是怎么来的——该算法来自于一篇87年的论文【5】, Percentage Closer 指的是在一个场景位置对应的一圈阴影贴图的像素上，像素的深度值比该场景位置的深度值距离光源更近（Closer）的像素数量的百分比（Percentage）；而 Filtering，是指多次比较求平均（或加权平均）的这个操作是一个滤波。

软阴影算法——Percentage Closer Soft Shadows（PCSS）

从图13(b)可以看到，虽然PCF是用于抗锯齿的，但阴影的边缘看上去已经是软阴影的样子了（有一个阴影过渡带）。但是，整个阴影的边缘的模糊程度是一致（Uniform）的，这和我们在实际生活中看到的不符（图14）。

图14，面光源下，球的正确的软阴影

从图12可以看出，如果我们将物体向墙壁移动，半影区的范围将缩小；正如图14所表现的一样：离球越近，阴影的过渡带越短。

这给了我们模拟真实的软阴影一个启发：既然PCF能让阴影变软，不同的滤波范围能产生不同的模糊效果；那么根据阴影离遮挡物（Blocker）的距离从近到远，我们使用对应的滤波范围也从小到大，不就能得到类似图14的效果了么？这正是软阴影算法 Percentage closer soft shadows 【6】的核心思路。

有了这个思路，只需要找到一个估计滤波范围（Filter size）的方法就好了。下面是 PCSS 的做法：

遮挡物搜索（Blocker search）：在阴影贴图的一个范围内找到比要渲染的位置（Receiver）的深度更近的深度，即遮挡物（Blocker）的深度，进行平均。搜索的范围取决于光源的大小和该位置到光源的距离。
半影区估计（Penumbra estimation）：利用刚才得到的遮挡物深度，估计半影区域的长度。
滤波：利用估计的半影区范围，来选择合适的滤波范围执行PCF算法。

具体的估计方法见图15：

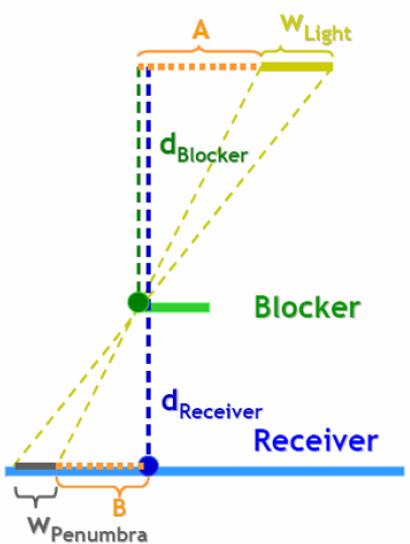
图15、PCSS算法(图源：Percentage-closer soft shadows)

图15中，光源和地板被认为是平行的， $w_{Penumbra}$ 即为半影区的长度， $w_{Light}$ 是光源的长度。可见，光源长度和半影区的长度分别在两个相似三角形上，因此可以得到半影区的长度的计算公式：

$w_{Penumbra}=\frac{(d_{Receiver} - d_{Blocker}) \cdot w_{Light}}d_{Blocker}$

图16为游戏《消逝的光芒》（Dying Light）中开启了PCSS的截图，可以从电线杆的影子中清晰的看到软阴影的变化。

图源：Nvidia 图片库图16、游戏《消逝的光芒》截图

方差阴影贴图（Variance Shadow Maps）

PCF的缺陷

PCF在每一次进行阴影计算时，是将阴影贴图的一个范围的所有像素的深度和一个阴影值 t 进行比较，再将比较的结果进行平均；这个平均后的结果，其实就是这个范围内，深度值大于 t 的像素的比例。正是为了得到这个比例，PCF查询（或采样）了这个范围内的所有像素，这种采样本身是非常耗时的；然而，为了能有好的效果，采样的范围却不能太小。能不能不查询（或采样）这个范围的像素呢？同时，显卡本身提供了内置的Mipmap以及各向异性滤波方法，用于对贴图进行模糊。那么，有没有办法让阴影的计算也能用上这种显卡内置的滤波能力呢？

方差阴影贴图的算法原理

方差阴影贴图算法[7]提出了一个大胆的想法：假设知道了这个范围内所有像素的深度的分布，那么我们就能很快的得到深度值大于 t 的像素的比例，从而不需要进行更多的采样。

那么深度的分布要怎么得到呢？方差阴影贴图找到了切比雪夫不等式（Chebyshev's Inequality）：

$P(x\geq t) \leq \frac{\sigma^2}{\sigma^2 + (t - \mu)^2}, \quad\text{for }t >$

其中， $\sigma$ 是分布的标准差， $\mu$ 是分布的均值， $P(x\geq t)$ 是大于 t 的值的比例。这个不等式告诉我们，如果我们知道了一个分布的均值和方差，那么对于大于均值的 t，我们可以立刻知道分布中比 t 大的值的最大比例。若直接用这个最大比例来估计阴影贴图的深度比较结果，我们不就可以立刻知道，对于一个位置，它是不是处于阴影之中了么？而对于 $t \leq \mu$ 的情况，方差阴影贴图算法直接认为这个位置是处于非阴影中的。

这样，我们就剩下了一个问题，要怎么方便的得到一个范围内的均值和方差？

均值好办，这可以用 Mipmaps 或者是求和面积表（Summed-area table）来进行快速计算。那么方差呢？且看下面的式子：

$\sigma^2 = E(x^2) - E(x)^2$

这个式子告诉我们，方差的计算可以用平方的均值减去均值的平方来得到。所以当计算阴影贴图中各个像素的深度的时候，同时计算深度的平方并保存下来，不就可以快速得到深度的平方的期望了么？如果深度占用了深度贴图的一个通道，深度的平方可以存放在未使用的其他通道，所以深度的平方的计算和保存，都可以在计算阴影贴图时很方便地“顺手”完成。同时，由于 $E(x^2)$ 和 $E(x)$ 是可以被插值的，所以显卡内置的滤波技术——Mipmapping和各项异性滤波——可以被用来降低阴影贴图的锯齿。

图源：Variance Shadow Maps 图17、VSM算法效果比较。从左到右分别为各个算法的效果：(a)标准的阴影映射；(b)5x5的PCF；(c)5x5的PCF，并在深度比较结果上进行2x2的双线性插值(d)VSM

图17为算法原论文中作者得到的结果：在GeForce 6800GT上，图17(d)中的VSM和图17(c)的效果类似，效率却是至少3倍以上。

VSM 的问题——以及MSM、CSM、ESM

当然了，VSM也有一些问题：将深度的分布都用均值和方差描述了，在方差比较大的时候，就容易出现原本不该有的非阴影部分（Light leaking）。

图源：pixelstoomany 图18、VSM的 Light bleeding 现象（水壶盖子周边的阴影被错误的计算，就像漏光一样）

这种 Light bleeding 现象，本质上还是使用切比雪夫不等式来对深度分布的估计过于简单。在数学中，矩（Moment）可以被用来描述随机变量的分布，比如随机变量的期望就是一阶矩，其方差就是二阶矩。在切比雪夫不等式中，我们只使用了一阶矩 $E(x)$ 和二阶矩 $\sigma^2$ ；就像泰勒展开的项数越多近似越准确一样，用越多不同阶的矩去近似一个分布，就能得到越准确的结果，这也就是矩阴影映射算法（Moment Shadow Mapping）[8]的思路。在使用前四阶矩的情况下，矩阴影映射算法可以得到非常不错的效果（图19）。

图19、阴影结果比较。左图：VSM；右图：MSM(图源：Moment Shadow Mapping)

卷积阴影贴图（Convolution Shadow Maps）[9]以及指数阴影贴图（Exponential Shadow Maps）[10]用了不同的思路去解决阴影映射的走样问题：相对于VSM的估计深度的分布，它们选择了去近似深度测试函数。其中，卷积阴影贴图使用了傅里叶级数来进行近似，这种方法不会产生漏光现象，并且可以得到很好的阴影效果，代价是需要将傅里叶级数的系数存在新的贴图中，大大增加了存储量；指数阴影贴图使用指数函数了来进行近似深度测试函数，避免了大量的存储开销，不过在阴影接收物的边界存在阴影不稳定的问题。

图20、左图：卷积阴影贴图结果(7x7 blur and mip-mapping)；右图：指数阴影贴图结果（using 5×5 Gauss filtering）

方差软阴影映射算法（Variance Soft Shadow Mapping）

方差阴影贴图算法解决了快速近似PCF的问题，如果要计算软阴影，还需要知道遮挡物搜索（Blocker search）要怎么做。

遮挡物搜索，其实就是在阴影贴图的一个范围内找到比一个值 t 小的像素，以这些像素的深度的平均值来作为遮挡物的深度。

图21、一个5x5大小的深度贴图的例子(图源：Games202)

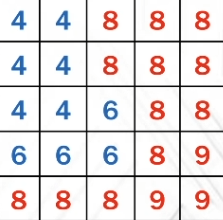
比如在图21中，假设我们的要查询的深度为7，那么深度比7更小的（蓝色的数字）就是遮挡物，我们记它们的平均深度为 $z_{occ}$ ；而红色的部分，我们记它们的平均深度为非遮挡物深度 $z_{unocc}$ 。

对于一个一共有 N 个点的范围，加入比 t 深度小的点共有 $N_1$ 个，深度大于等于 t 的点共有 $N_2$ 个，那么有下面这样的等式：

$\frac{N_1}{N} z_{occ} + \frac{N_2}{N}z_{unocc} = z_{avg}$

其中 $z_{avg}$ 是深度的平均值。在上面的等式中，只有 $z_{avg}$ 和 N 是我们知道的，要怎么得到 $z_{occ}$ 呢？

首先看 $\frac{N_2}{N}$ ，这是深度大于等于 t 的点的比例，这不就是我们刚刚在切比雪夫不等式中的 $P(x\geq t)$ 么？而如果 $\frac{N_2}{N}$ 已经知道了， $\frac{N_1}{N}$ 也就自然知道了（ $1 - \frac{N_2}{N}$ ）。接下来，只要再做一个大胆的假设： $z_{unocc}=t$ ，那么 $z_{occ}$ 就可以很方便地计算出来了！

$z_{unocc}=t$ 这个近似，相当于是说阴影的接收点处于一个和光源平行的平面，所以当这个条件不满足的时候，这个近似就不够准确了。虽然如此，在一般情况下，VSSM都可以得到很好的结果（图22）

图22、VSSM算法得到的软阴影(图源: GPUGems3 - Chapter 8)

结语

本文的内容框架来自于一个非常棒的实时渲染在线课程 Games 202 的第三讲及第四讲，十分推荐。文章中用到的参考链接及参考文献已被列在了文章末尾。

参考链接

Games 202
维基百科的Shadow mapping
GPUGems chapter 11-shadow-map-antialiasing
GPUGems3 chapter-10-parallel-split-shadow-maps-programmable-gpus
GPUGems3 - Chapter 8
https://learnopengl.com/Advanced-Lighting/Shadows/Shadow-Mapping

参考文献

[1] Williams L. Casting curved shadows on curved surfaces[C]//Proceedings of the 5th annual conference on Computer graphics and interactive techniques. 1978: 270-274.
[2] Stamminger M, Drettakis G. Perspective shadow maps[C]//Proceedings of the 29th annual conference on Computer graphics and interactive techniques. 2002: 557-562.
[3] Fernando R, Fernandez S, Bala K, et al. Adaptive shadow maps[C]//Proceedings of the 28th annual conference on Computer graphics and interactive techniques. 2001: 387-390.
[4] Zhang F, Sun H, Xu L, et al. Parallel-split shadow maps for large-scale virtual environments[C]//Proceedings of the 2006 ACM international conference on Virtual reality continuum and its applications. 2006: 311-318.
[5] Reeves W T, Salesin D H, Cook R L. Rendering antialiased shadows with depth maps[C]//Proceedings of the 14th annual conference on Computer graphics and interactive techniques. 1987: 283-291.
[6] Fernando R. Percentage-closer soft shadows[M]//ACM SIGGRAPH 2005 Sketches. 2005: 35-es.
[7] Donnelly W, Lauritzen A. Variance shadow maps[C]//Proceedings of the 2006 symposium on Interactive 3D graphics and games. 2006: 161-165.
[8] Peters C, Klein R. Moment shadow mapping[C]//Proceedings of the 19th Symposium on Interactive 3D Graphics and Games. 2015: 7-14.
[9] Annen T, Mertens T, Bekaert P, et al. Convolution Shadow Maps[J]. Rendering Techniques, 2007, 18: 51-60.
[10] Annen T, Mertens T, Seidel H P, et al. Exponential shadow maps[C]//Graphics Interface. ACM Press, 2008: 155-161.

wizlyk

ShadowAlgorithms